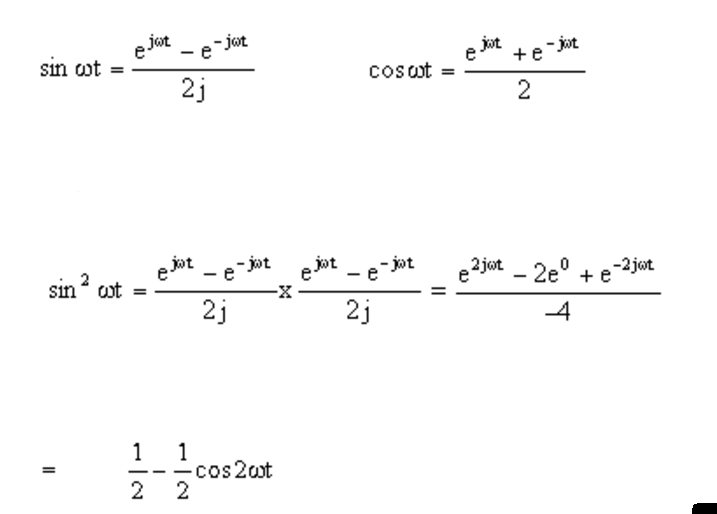
Cosine In Exponential Form

Cosine In Exponential Form - Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Web integrals of the form z cos(ax)cos(bx)dx; Web the fourier series can be represented in different forms. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Cosz = exp(iz) + exp( − iz) 2. Web relations between cosine, sine and exponential functions. As a result, the other hyperbolic functions are meromorphic in the whole complex plane. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: For any complex number z ∈ c :

Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Cosz denotes the complex cosine. Web integrals of the form z cos(ax)cos(bx)dx; Using these formulas, we can. Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & = & (e^{i \theta})^2 \\ & = & (\cos\theta+i\sin\theta)^2 \\ & = & (\cos\theta)^2+2i\cos θ\sin. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Andromeda on 10 nov 2021. Expz denotes the exponential function. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and.

Cosz = exp(iz) + exp( − iz) 2. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: The sine of the complement of a given angle or arc. Andromeda on 10 nov 2021. (in a right triangle) the ratio of the side adjacent to a given angle to the hypotenuse. Using these formulas, we can. I am trying to convert a cosine function to its exponential form but i do not know how to do it. Web the hyperbolic sine and the hyperbolic cosine are entire functions. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and.

EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube

As a result, the other hyperbolic functions are meromorphic in the whole complex plane. Web relations between cosine, sine and exponential functions. (in a right triangle) the ratio of the side adjacent to a given angle to the hypotenuse. Andromeda on 10 nov 2021. The sine of the complement of a given angle or arc.

Basics of QPSK modulation and display of QPSK signals Electrical

The sine of the complement of a given angle or arc. Andromeda on 10 nov 2021. Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & = & (e^{i \theta})^2 \\ & = & (\cos\theta+i\sin\theta)^2 \\ & = & (\cos\theta)^2+2i\cos θ\sin. For any complex number z ∈ c : Web the fourier series can be represented in different forms.

Solution One term of a Fourier series in cosine form is 10 cos 40πt

Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & = & (e^{i \theta})^2 \\ & = & (\cos\theta+i\sin\theta)^2 \\ & = & (\cos\theta)^2+2i\cos θ\sin. Web relations between cosine, sine and exponential functions. Web the fourier series can be represented in different forms. Web integrals of the form z cos(ax)cos(bx)dx; I am trying to convert a cosine function to its exponential form.

Other Math Archive January 29, 2018

Cosz denotes the complex cosine. Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & = & (e^{i \theta})^2 \\ & = & (\cos\theta+i\sin\theta)^2 \\ & = & (\cos\theta)^2+2i\cos θ\sin. Web the fourier series can be represented in different forms. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. The sine of the complement of a given angle or arc.

PPT Fourier Series PowerPoint Presentation ID390675

(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Cosz denotes the complex cosine. As a result, the other hyperbolic functions are meromorphic in the whole complex plane. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Andromeda on 10 nov 2021.

Question Video Converting the Product of Complex Numbers in Polar Form

As a result, the other hyperbolic functions are meromorphic in the whole complex plane. Cosz denotes the complex cosine. Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & = & (e^{i \theta})^2 \\ & = & (\cos\theta+i\sin\theta)^2 \\ & = & (\cos\theta)^2+2i\cos θ\sin. Web the fourier series can be represented in different forms. I am trying to convert a cosine function.

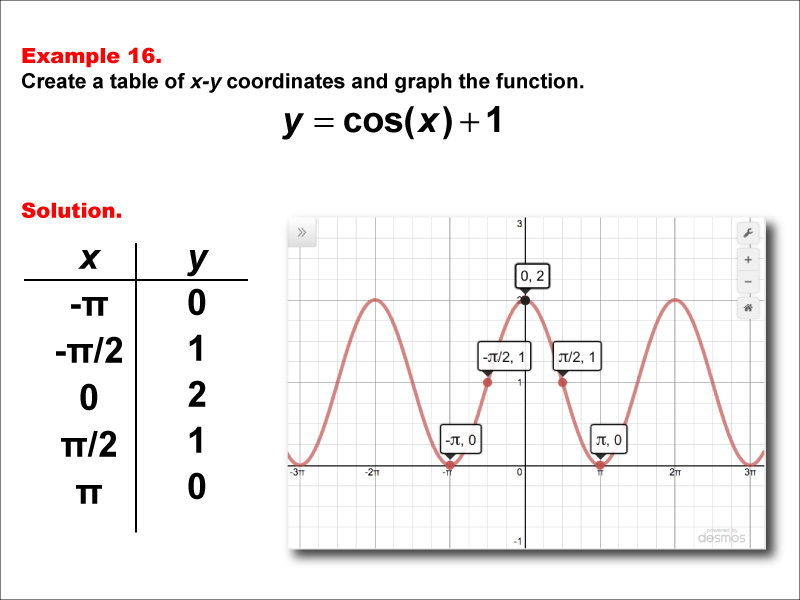
Math Example Cosine Functions in Tabular and Graph Form Example 16

The sine of the complement of a given angle or arc. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: Web relations between cosine, sine and exponential functions. Expz denotes the exponential function. Web integrals of the form z cos(ax)cos(bx)dx;

Relationship between sine, cosine and exponential function

Web integrals of the form z cos(ax)cos(bx)dx; Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & =.

Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube

(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Using these formulas, we can. Web the fourier series can be represented in different forms. Web relations between cosine, sine and exponential functions. Expz denotes the exponential function.

Exponential cosine fit A phase binned amplitude exemplar (Data) is

For any complex number z ∈ c : The sine of the complement of a given angle or arc. Cosz = exp(iz) + exp( − iz) 2. Web integrals of the form z cos(ax)cos(bx)dx; Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and.

Web Using The Exponential Forms Of Cos(Theta) And Sin(Theta) Given In (3.11A, B), Prove The Following Trigonometric Identities:

Web relations between cosine, sine and exponential functions. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$.

Using These Formulas, We Can.

Cosz = exp(iz) + exp( − iz) 2. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Web the hyperbolic sine and the hyperbolic cosine are entire functions. Web integrals of the form z cos(ax)cos(bx)dx;

Web Euler’s Formula For Complex Exponentials According To Euler, We Should Regard The Complex Exponential Eit As Related To The Trigonometric Functions Cos(T) And.

Web $\begin{array}{lcl}\cos(2\theta)+i\sin(2\theta) & = & e^{2i\theta} \\ & = & (e^{i \theta})^2 \\ & = & (\cos\theta+i\sin\theta)^2 \\ & = & (\cos\theta)^2+2i\cos θ\sin. The sine of the complement of a given angle or arc. I am trying to convert a cosine function to its exponential form but i do not know how to do it. Cosz denotes the complex cosine.

Web The Fourier Series Can Be Represented In Different Forms.

(in a right triangle) the ratio of the side adjacent to a given angle to the hypotenuse. Expz denotes the exponential function. For any complex number z ∈ c : Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions.