Rank Row Echelon Form
Rank Row Echelon Form - Web matrix rank is calculated by reducing matrix to a row echelon form using elementary row operations. Then the rank of the matrix is equal to the number of non. Web here are the steps to find the rank of a matrix. Each leading entry is in a. Web using mathematical induction, the author provides a simple proof that the reduced row echelon form of a matrix is unique. Web rank of matrix. Web the rank is equal to the number of pivots in the reduced row echelon form, and is the maximum number of linearly independent columns that can be chosen from the matrix. A pdf copy of the article can be viewed by clicking. Web 1 the key point is that two vectors like v1 = (a1,b1,c1, ⋯) v 1 = ( a 1, b 1, c 1, ⋯) v2 = (0,b2,c2, ⋯) v 2 = ( 0, b 2, c 2, ⋯) can't be linearly dependent for a1 ≠ 0 a 1 ≠ 0. Use row operations to find a matrix in row echelon form that is row equivalent to [a b].
Convert the matrix into echelon form using row/column transformations. [1 0 0 0 0 1 − 1 0]. Web 1 the key point is that two vectors like v1 = (a1,b1,c1, ⋯) v 1 = ( a 1, b 1, c 1, ⋯) v2 = (0,b2,c2, ⋯) v 2 = ( 0, b 2, c 2, ⋯) can't be linearly dependent for a1 ≠ 0 a 1 ≠ 0. Pivot numbers are just the. Web matrix rank is calculated by reducing matrix to a row echelon form using elementary row operations. Web using mathematical induction, the author provides a simple proof that the reduced row echelon form of a matrix is unique. Web row echelon form natural language math input extended keyboard examples assuming row echelon form refers to a computation | use as referring to a mathematical. A pdf copy of the article can be viewed by clicking. Each leading entry is in a. Web the rank is equal to the number of pivots in the reduced row echelon form, and is the maximum number of linearly independent columns that can be chosen from the matrix.
Web to find the rank of a matrix, we will transform the matrix into its echelon form. Convert the matrix into echelon form using row/column transformations. Then the rank of the matrix is equal to the number of non. [1 0 0 0 0 1 − 1 0]. Web matrix rank is calculated by reducing matrix to a row echelon form using elementary row operations. Web 1 the key point is that two vectors like v1 = (a1,b1,c1, ⋯) v 1 = ( a 1, b 1, c 1, ⋯) v2 = (0,b2,c2, ⋯) v 2 = ( 0, b 2, c 2, ⋯) can't be linearly dependent for a1 ≠ 0 a 1 ≠ 0. Web row echelon form natural language math input extended keyboard examples assuming row echelon form refers to a computation | use as referring to a mathematical. Web the rank is equal to the number of pivots in the reduced row echelon form, and is the maximum number of linearly independent columns that can be chosen from the matrix. Use row operations to find a matrix in row echelon form that is row equivalent to [a b]. Assign values to the independent variables and use back substitution.
Tricks to find rank of matrix by Echelon Form (Tricks for RowEchelon
Web a matrix is in row echelon form (ref) when it satisfies the following conditions. Assign values to the independent variables and use back substitution. Web rank of matrix. To find the rank, we need to perform the following steps: Web row echelon form natural language math input extended keyboard examples assuming row echelon form refers to a computation |.
Augmented Matrices Row Echelon Form YouTube
Convert the matrix into echelon form using row/column transformations. Web rank of matrix. Web using mathematical induction, the author provides a simple proof that the reduced row echelon form of a matrix is unique. Web a matrix is in row echelon form (ref) when it satisfies the following conditions. [1 0 0 0 0 1 − 1 0].
Solved Find the reduced row echelon form of the following
Web to find the rank of a matrix, we will transform the matrix into its echelon form. Web rank of matrix. Convert the matrix into echelon form using row/column transformations. Web using mathematical induction, the author provides a simple proof that the reduced row echelon form of a matrix is unique. A pdf copy of the article can be viewed.
class 12 Rank Row Echelon Form YouTube
Web to find the rank of a matrix, we will transform the matrix into its echelon form. A pdf copy of the article can be viewed by clicking. Web 1 the key point is that two vectors like v1 = (a1,b1,c1, ⋯) v 1 = ( a 1, b 1, c 1, ⋯) v2 = (0,b2,c2, ⋯) v 2 =.
Echelon Form of a matrix to find rank YouTube
In the case of the row echelon form matrix, the. Then the rank of the matrix is equal to the number of non. Web row echelon form natural language math input extended keyboard examples assuming row echelon form refers to a computation | use as referring to a mathematical. Pivot numbers are just the. To find the rank, we need.
Solved Are The Following Matrices In Reduced Row Echelon
Use row operations to find a matrix in row echelon form that is row equivalent to [a b]. Assign values to the independent variables and use back substitution. [1 0 0 0 0 1 − 1 0]. Web a matrix is in row echelon form (ref) when it satisfies the following conditions. Then the rank of the matrix is equal.
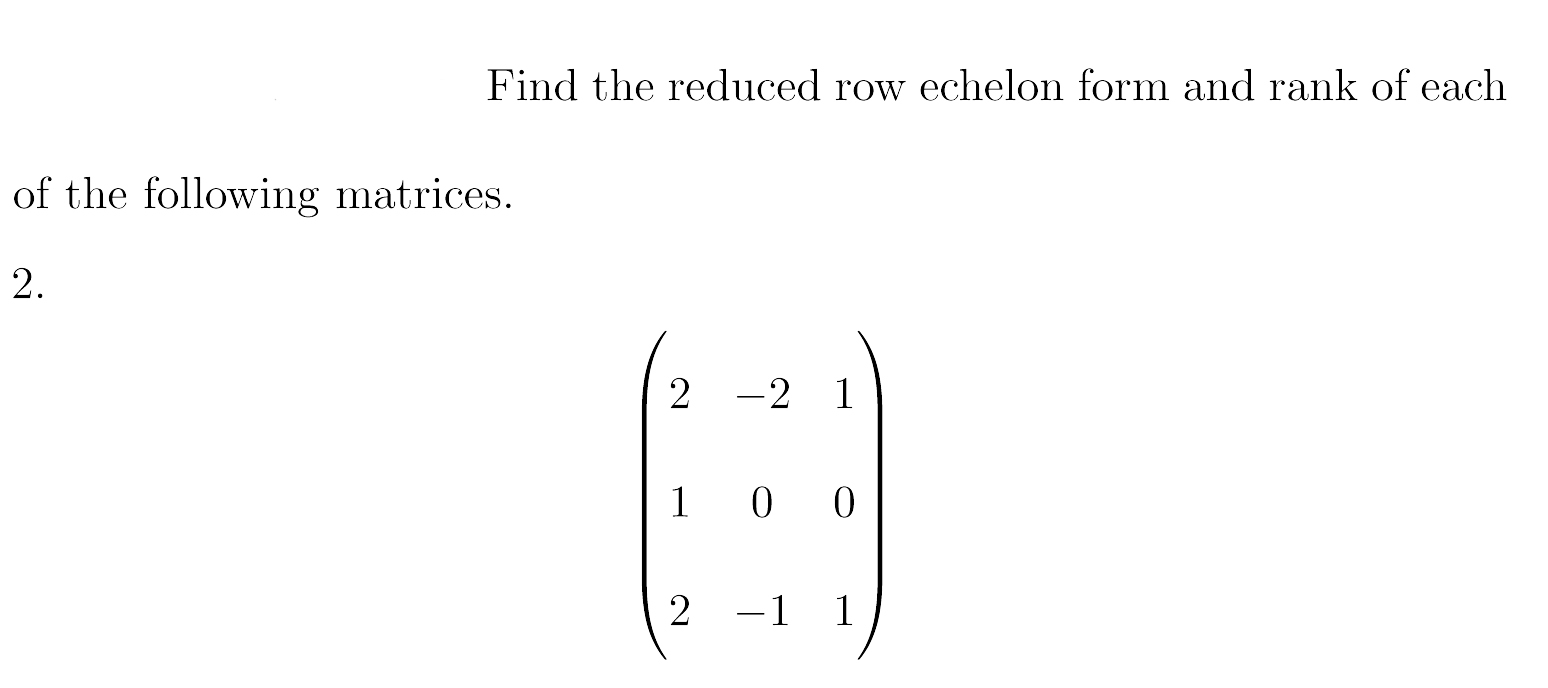
Solved Find the reduced row echelon form and rank of each of
To find the rank, we need to perform the following steps: [1 0 0 0 0 1 − 1 0]. Each leading entry is in a. Web here are the steps to find the rank of a matrix. Assign values to the independent variables and use back substitution.
Note Set 10a a Reduced Row Echelon Form Whisperer Matrixology
Use row operations to find a matrix in row echelon form that is row equivalent to [a b]. Web using mathematical induction, the author provides a simple proof that the reduced row echelon form of a matrix is unique. [1 0 0 0 0 1 − 1 0]. Web matrix rank is calculated by reducing matrix to a row echelon.
matrix rank Why do I get differnt row reduced echelon form
Use row operations to find a matrix in row echelon form that is row equivalent to [a b]. Web the rank is equal to the number of pivots in the reduced row echelon form, and is the maximum number of linearly independent columns that can be chosen from the matrix. Web using mathematical induction, the author provides a simple proof.
Elementary Linear Algebra Echelon Form of a Matrix, Part 1 YouTube
Web matrix rank is calculated by reducing matrix to a row echelon form using elementary row operations. Each leading entry is in a. Web to find the rank of a matrix, we will transform the matrix into its echelon form. Web 1 the key point is that two vectors like v1 = (a1,b1,c1, ⋯) v 1 = ( a 1,.
Web Here Are The Steps To Find The Rank Of A Matrix.
Each leading entry is in a. Web matrix rank is calculated by reducing matrix to a row echelon form using elementary row operations. A pdf copy of the article can be viewed by clicking. In the case of the row echelon form matrix, the.
Web A Matrix Is In Row Echelon Form (Ref) When It Satisfies The Following Conditions.
Web using mathematical induction, the author provides a simple proof that the reduced row echelon form of a matrix is unique. Use row operations to find a matrix in row echelon form that is row equivalent to [a b]. Web 1 the key point is that two vectors like v1 = (a1,b1,c1, ⋯) v 1 = ( a 1, b 1, c 1, ⋯) v2 = (0,b2,c2, ⋯) v 2 = ( 0, b 2, c 2, ⋯) can't be linearly dependent for a1 ≠ 0 a 1 ≠ 0. Assign values to the independent variables and use back substitution.
Convert The Matrix Into Echelon Form Using Row/Column Transformations.
Web rank of matrix. Then the rank of the matrix is equal to the number of non. [1 0 0 0 0 1 − 1 0]. Web the rank is equal to the number of pivots in the reduced row echelon form, and is the maximum number of linearly independent columns that can be chosen from the matrix.
Pivot Numbers Are Just The.
Web to find the rank of a matrix, we will transform the matrix into its echelon form. Web row echelon form natural language math input extended keyboard examples assuming row echelon form refers to a computation | use as referring to a mathematical. To find the rank, we need to perform the following steps: