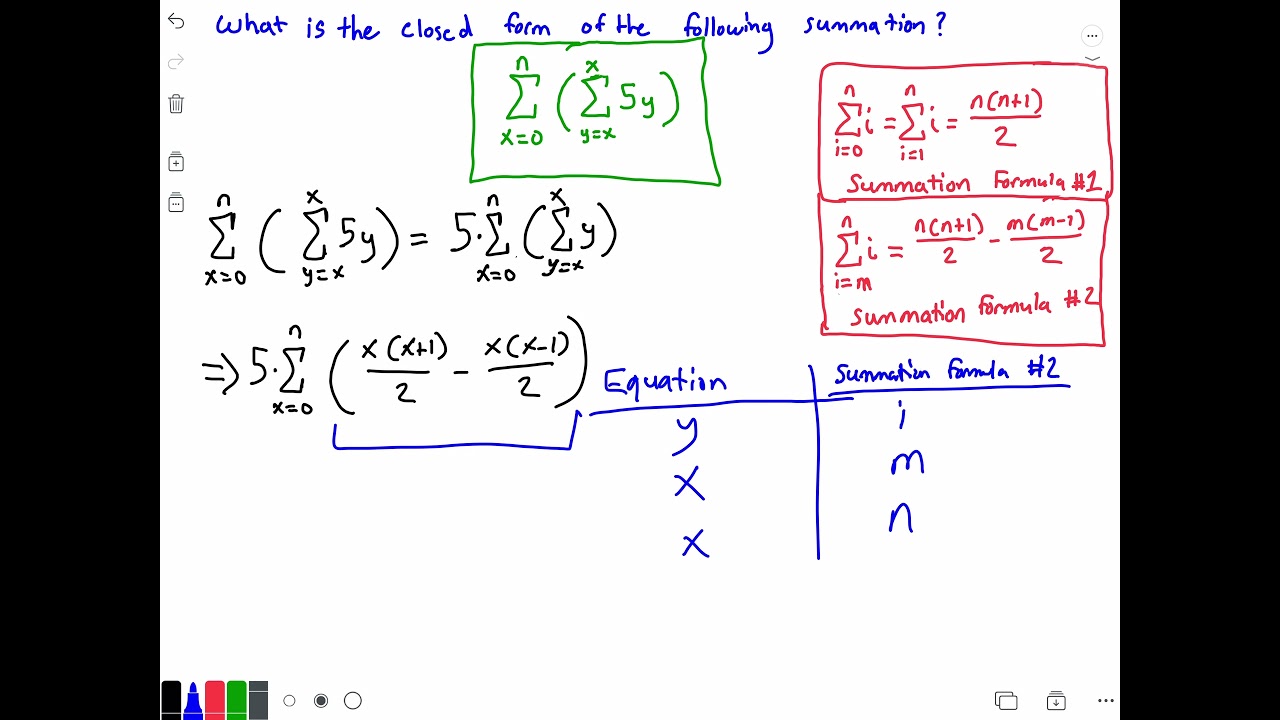
Summation Closed Form
Summation Closed Form - Modified 8 years, 3 months ago. However, the book concrete mathematics , by graham,. ∑i=1n (ai + b) ∑ i = 1 n ( a i + b) let n ≥ 1 n ≥ 1 be an. For your particular series, if i am correct in assuming. Web to answer the question you asked, there is not in general a method for converting a summation to closed form. Web closed form summation sep 13, 2010 #1 mcbballp32 3 0 ignore the above, i was haveing problems with the symbol. How to use the summation calculator. Asked 8 years, 3 months ago. For example for (int i=0;i<n;i++) result += i; Summation videos:closed form solution summation:
How to use the summation calculator. Web closed form summation example. Web determine a closed form solution for the summation. ∑i=1n (ai + b) ∑ i = 1 n ( a i + b) let n ≥ 1 n ≥ 1 be an. If f ( i ). I understand the goal at hand, but do not understand the process for. Just enter the expression to. Web to answer the question you asked, there is not in general a method for converting a summation to closed form. Let's first briefly define summation notation. Web 3 i am struggling to understand basics as it related to forming a closed form expression from a summation.
Web closed form summation example. Just enter the expression to. For example for (int i=0;i<n;i++) result += i; Web 3 i am struggling to understand basics as it related to forming a closed form expression from a summation. Web often a summation can be converted to a closed form solution. However, the book concrete mathematics , by graham,. Web you can use this summation calculator to rapidly compute the sum of a series for certain expression over a predetermined range. Modified 8 years, 3 months ago. The closed form sum of $$12 \left[ 1^2 \cdot 2 + 2^2 \cdot 3 + \ldots + n^2 (n+1) \right]$$ for $n \geq 1$ is $n(n+1)(n+2)(an+b).$ find $an + b.$ how. Web loosely speaking, a discrete function is of closed form if it shares certain essential properties with the hypergeometric function , a function which itself is defined to.
Solved Question 1 1) Find A Closed Form For The Double S...
Just enter the expression to. For your particular series, if i am correct in assuming. However, the book concrete mathematics , by graham,. ∑i=1n (ai + b) ∑ i = 1 n ( a i + b) let n ≥ 1 n ≥ 1 be an. The closed form sum of $$12 \left[ 1^2 \cdot 2 + 2^2 \cdot 3.
Summation Closed Form Solution YouTube
Web often a summation can be converted to a closed form solution. Web you can use this summation calculator to rapidly compute the sum of a series for certain expression over a predetermined range. The closed form sum of $$12 \left[ 1^2 \cdot 2 + 2^2 \cdot 3 + \ldots + n^2 (n+1) \right]$$ for $n \geq 1$ is $n(n+1)(n+2)(an+b).$.
Solved Question 1 1) Find A Closed Form For The Double S...
However, the book concrete mathematics , by graham,. Convert each to closed form: Web summation closed form. Summation videos:closed form solution summation: For your particular series, if i am correct in assuming.
Put The Summation In Closed Form YouTube
Web summation closed form. For your particular series, if i am correct in assuming. The closed form sum of $$12 \left[ 1^2 \cdot 2 + 2^2 \cdot 3 + \ldots + n^2 (n+1) \right]$$ for $n \geq 1$ is $n(n+1)(n+2)(an+b).$ find $an + b.$ how. Web loosely speaking, a discrete function is of closed form if it shares certain essential.
Solved Compute the following summations. ( Instructions
Web loosely speaking, a discrete function is of closed form if it shares certain essential properties with the hypergeometric function , a function which itself is defined to. Web often a summation can be converted to a closed form solution. I understand the goal at hand, but do not understand the process for. Just enter the expression to. Asked 8.
notation Closed form expressions for a sum Mathematics Stack Exchange
Web 3 i am struggling to understand basics as it related to forming a closed form expression from a summation. Web loosely speaking, a discrete function is of closed form if it shares certain essential properties with the hypergeometric function , a function which itself is defined to. Web determine a closed form solution for the summation. Asked 8 years,.
(PDF) Closedform summation of the Dowker and related sums
For your particular series, if i am correct in assuming. However, the book concrete mathematics , by graham,. I understand the goal at hand, but do not understand the process for. Web closed form summation example. For example for (int i=0;i<n;i++) result += i;
summation Does this sum/product have a closed form? f(x)=\sum
Web summation notation is used to define the definite integral of a continuous function of one variable on a closed interval. Convert each to closed form: Web summation closed form. Modified 8 years, 3 months ago. Summation videos:closed form solution summation:
calculus A closed form for the sum of (e(1+1/n)^n) over n
For your particular series, if i am correct in assuming. ∑ j = 0 ⌊ i + n − 1 n + 2 ⌋ ( − 1) j ( n j) ( i + n − j ( n + 2) − 1 n − 1) + ∑ j = 0 ⌊ i + n − 2 n + 2.
PCH Section 8.1 Closed Form Summation Example YouTube
Just enter the expression to. Web often a summation can be converted to a closed form solution. The closed form sum of $$12 \left[ 1^2 \cdot 2 + 2^2 \cdot 3 + \ldots + n^2 (n+1) \right]$$ for $n \geq 1$ is $n(n+1)(n+2)(an+b).$ find $an + b.$ how. Web summation notation is used to define the definite integral of a.
If F ( I ).
How to use the summation calculator. Web summation notation is used to define the definite integral of a continuous function of one variable on a closed interval. Web you can use this summation calculator to rapidly compute the sum of a series for certain expression over a predetermined range. Web closed form summation sep 13, 2010 #1 mcbballp32 3 0 ignore the above, i was haveing problems with the symbol.
I Understand The Goal At Hand, But Do Not Understand The Process For.
Web loosely speaking, a discrete function is of closed form if it shares certain essential properties with the hypergeometric function , a function which itself is defined to. Web closed form summation example. Web determine a closed form solution for the summation. Web often a summation can be converted to a closed form solution.
Let's First Briefly Define Summation Notation.
Just enter the expression to. Convert each to closed form: Web to answer the question you asked, there is not in general a method for converting a summation to closed form. ∑i=1n (ai + b) ∑ i = 1 n ( a i + b) let n ≥ 1 n ≥ 1 be an.
Asked 8 Years, 3 Months Ago.
The closed form sum of $$12 \left[ 1^2 \cdot 2 + 2^2 \cdot 3 + \ldots + n^2 (n+1) \right]$$ for $n \geq 1$ is $n(n+1)(n+2)(an+b).$ find $an + b.$ how. Modified 8 years, 3 months ago. Web 3 i am struggling to understand basics as it related to forming a closed form expression from a summation. For example for (int i=0;i<n;i++) result += i;