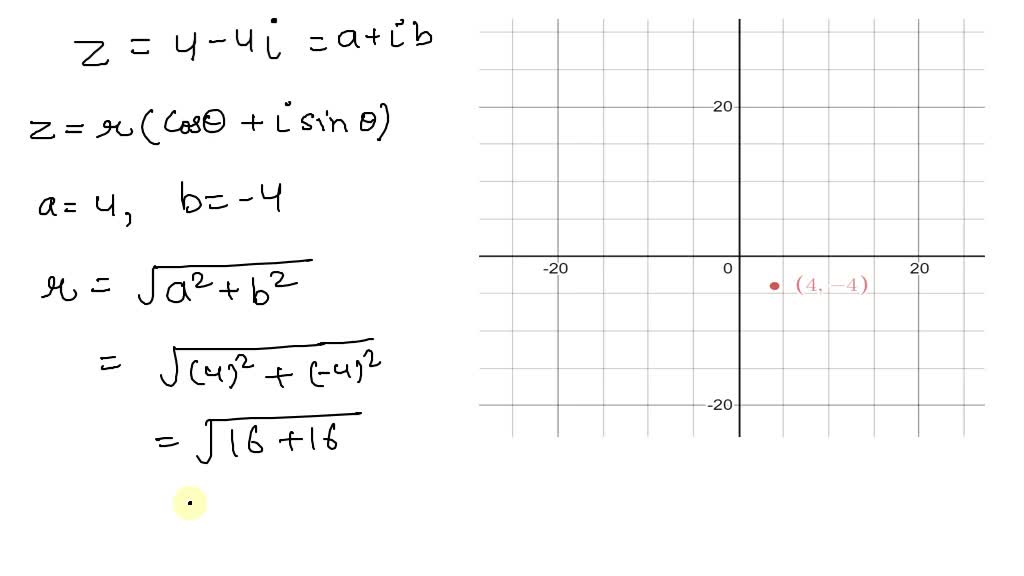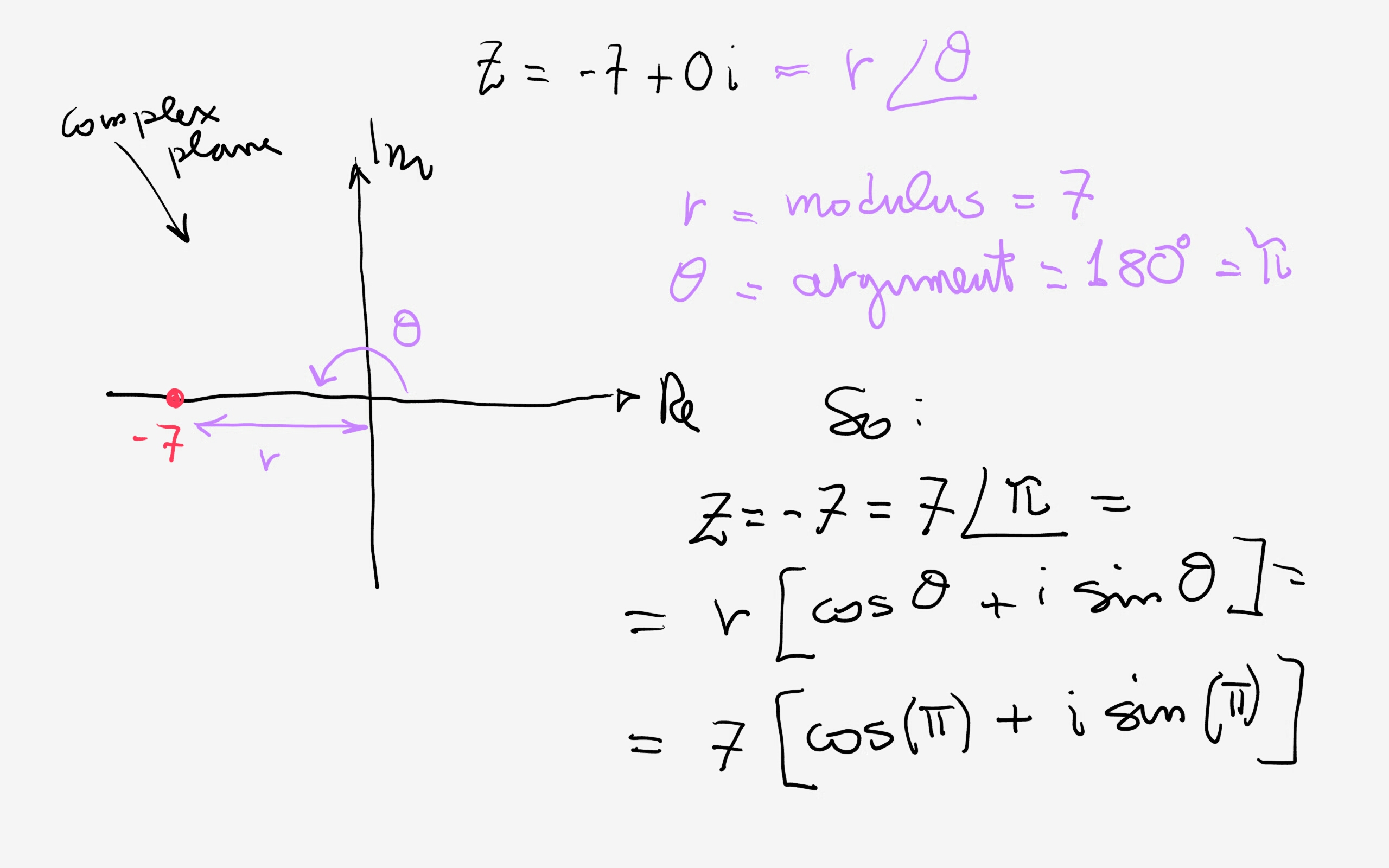Trigonometric Form Of A Complex Number
Trigonometric Form Of A Complex Number - Θ1 = arctan(1) = π 4 and ρ1 = √1 + 1 = √2. As a consequence, we will be able to quickly calculate powers of complex numbers, and even roots of complex numbers. = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you to make sure is in the correct quadrant. Web depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). Web trigonometric form of a complex number. Web this trigonometric form connects algebra to trigonometry and will be useful for quickly and easily finding powers and roots of complex numbers. Put these complex numbers in trigonometric form. Enter the complex number for which you want to find the trigonometric form. Use the trigonometric form of z.
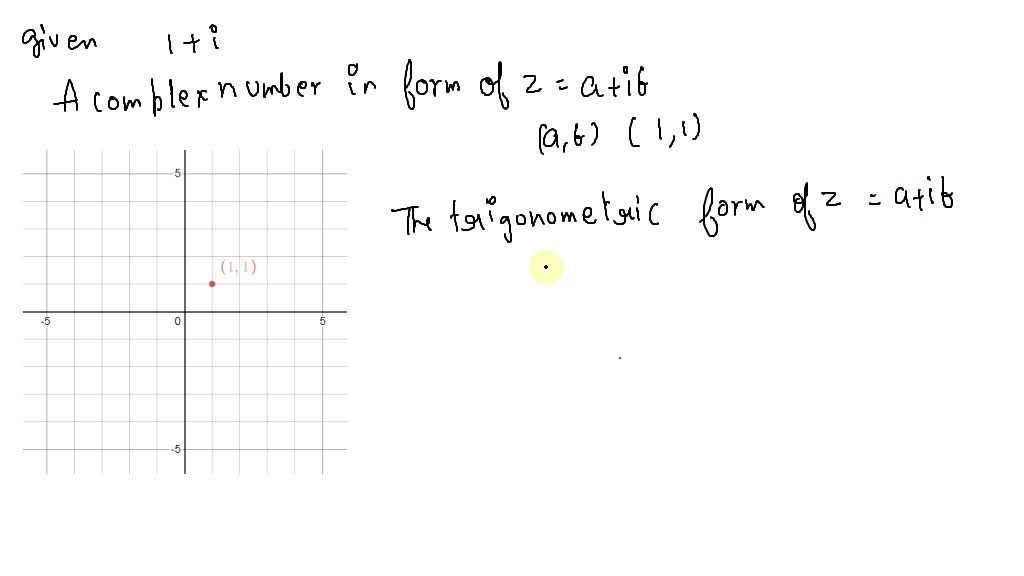
Trigonometric form of a complex number. Normally, examples write the following complex numbers in trigonometric form: Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Θ2 = arctan( 1 √3) = π 6 and ρ2 = √3 +1 = 2. Click the blue arrow to submit. Web trigonometric form of a complex number mario's math tutoring 285k subscribers join subscribe 1.1k share save 105k views 7 years ago imaginary & complex numbers learn how to convert a. Web the trigonometric form of a complex number z = a + bi is = r(cos i sin ); Trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point. For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. Note the word polar here comes from the fact that this process can be viewed as occurring with polar coordinates.
Note the word polar here comes from the fact that this process can be viewed as occurring with polar coordinates. Beginning activity let z = r(cos(θ) + isin(θ)). Web trigonometric form of a complex number mario's math tutoring 285k subscribers join subscribe 1.1k share save 105k views 7 years ago imaginary & complex numbers learn how to convert a. Find |z| | z |. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Where r = ja + bij is the modulus of z, and tan we will require 0 < 2. Choose convert to trigonometric form from the topic selector and click to see the result in our algebra. Use the trigonometric form of z. 4 + 4i to write the number in trigonometric form, we need r and.
SOLVEDTrigonometric Form of a Complex Number Rep…
The modulus of a complex number is the distance from the origin on the complex plane. Where r = ja + bij is the modulus of z, and tan we will require 0 < 2. For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. Let's compute the two trigonometric forms: = a.
The Product and Quotient of Complex Numbers in Trigonometric Form YouTube
Click the blue arrow to submit. Web depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. Normally, examples write the following complex numbers in trigonometric form: Put these complex numbers in trigonometric form. For example, let z1 = 1 + i, z2 = √3 +i and z3 =.
Trigonometric Form of a Complex Number Represent
4 + 4i to write the number in trigonometric form, we need r and. Web the trigonometric form of a complex number provides a relatively quick and easy way to compute products of complex numbers. Web depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. Web this trigonometric.
How do you express the complex number in trigonometric form 2+(sqrt 3
Enter the complex number for which you want to find the trigonometric form. Beginning activity let z = r(cos(θ) + isin(θ)). Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. As a consequence, we will be able to quickly calculate.
Trigonometric Form Into A Complex Number
Web any point represented in the complex plane as a + b i can be represented in polar form just like any point in the rectangular coordinate system. Θ2 = arctan( 1 √3) = π 6 and ρ2 = √3 +1 = 2. Θ1 = arctan(1) = π 4 and ρ1 = √1 + 1 = √2. Web this is.
How do you write the complex number in trigonometric form 7? Socratic
Web any point represented in the complex plane as a + b i can be represented in polar form just like any point in the rectangular coordinate system. Web depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny. Find |z| | z |. Click the blue arrow to.
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
Let's compute the two trigonometric forms: Web trigonometric form of a complex number. Put these complex numbers in trigonometric form. Web the trigonometric form of a complex number z = a + bi is = r(cos i sin ); Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ.
Complex Numbers in Trigonometric Form YouTube
Θ2 = arctan( 1 √3) = π 6 and ρ2 = √3 +1 = 2. Trigonometric form of a complex number. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). The modulus of a complex number is the distance from the origin on the complex plane..
PPT Trigonometric Form of a Complex Number PowerPoint Presentation
For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. Normally, examples write the following complex numbers in trigonometric form: Web this trigonometric form connects algebra to trigonometry and will be useful for quickly and easily finding powers and roots of complex numbers. Web trigonometric form of a complex number mario's math tutoring.
Multiplying Complex Numbers In Trigonometric Form YouTube
Use the trigonometric form of z. Beginning activity let z = r(cos(θ) + isin(θ)). For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). = a + bi becomes z.
Θ1 = Arctan(1) = Π 4 And Ρ1 = √1 + 1 = √2.
The complex number trigonometric form calculator converts complex numbers to their trigonometric form. Put these complex numbers in trigonometric form. Web this is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. As a consequence, we will be able to quickly calculate powers of complex numbers, and even roots of complex numbers.
Where R = Ja + Bij Is The Modulus Of Z, And Tan We Will Require 0 < 2.
Web the trigonometric form of a complex number z = a + bi is = r(cos i sin ); Θ2 = arctan( 1 √3) = π 6 and ρ2 = √3 +1 = 2. Choose convert to trigonometric form from the topic selector and click to see the result in our algebra. Web depending on what you need to do with your complex numbers, the trigonometric form can be very useful or very thorny.
= A + Bi Becomes Z = R(Cos + Isin ) = |Z| And The Reference Angle, ' Is Given By Tan ' = |B/A| Note That It Is Up To You To Make Sure Is In The Correct Quadrant.
Normally, examples write the following complex numbers in trigonometric form: Trigonometric form of a complex number. = b is called the argument of z. Use the trigonometric form of z.
For Example, Let Z1 = 1 + I, Z2 = √3 +I And Z3 = −1 +I√3.
Web any point represented in the complex plane as a + b i can be represented in polar form just like any point in the rectangular coordinate system. Web the trigonometric form of a complex number provides a relatively quick and easy way to compute products of complex numbers. Note the word polar here comes from the fact that this process can be viewed as occurring with polar coordinates. Trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point.