Which Of The Following Matrices Are In Row Reduced Form
Which Of The Following Matrices Are In Row Reduced Form - [5] it is in row echelon form. Web learn which row reduced matrices come from inconsistent linear systems. Multiplying a row by a constant: Identify the leading 1s in the following matrix: Consider the matrix a given by. If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. Web the final matrix is in reduced row echelon form. Web how to solve a system in reduced echelon form. Adding a constant times a row to another row: Row operation, row equivalence, matrix,.
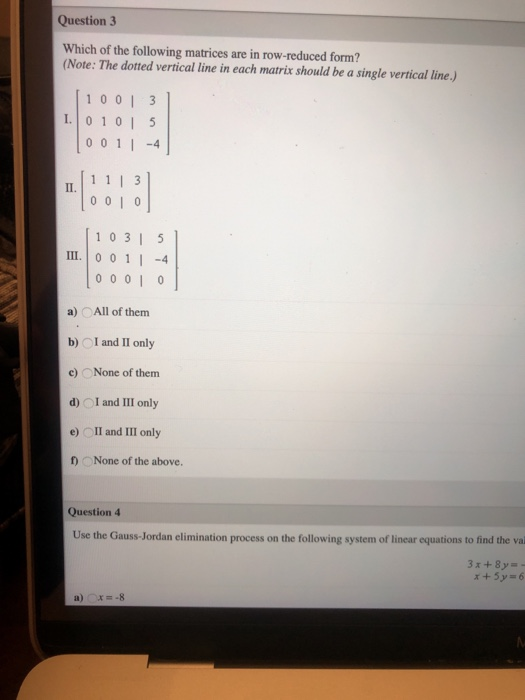
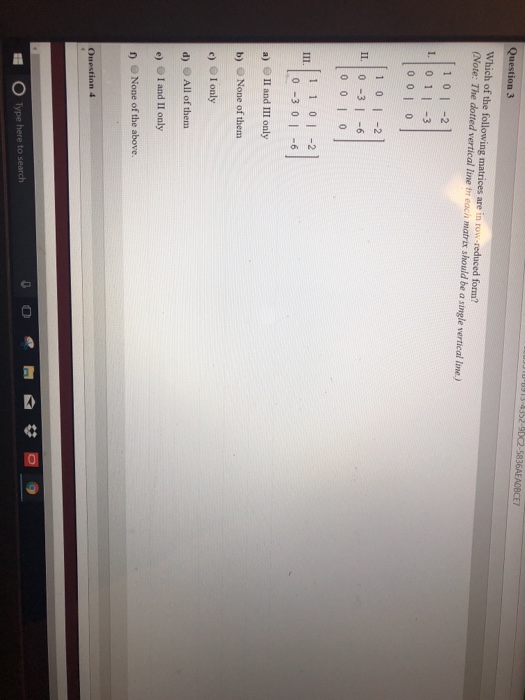
Web then there exists an invertible matrix p such that pa = r and an invertible matrix q such that qr^t qrt is the reduced row echelon form of r^t rt. Multiplying a row by a constant: The dotted vertical line in each matrix should be a single vertical line.) i. This problem has been solved!. Identify the leading 1s in the following matrix: B) i and ii only. The leading entry in each nonzero. Web learn which row reduced matrices come from inconsistent linear systems. [ 1 0 0 1 0 1. Web a matrix is in row reduced echelon formif the following conditions are satisfied:
If m is a sufficiently non ‐ degenerate. Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. Web give one reason why one might not be interested in putting a matrix into reduced row echelon form. Web a matrix is in row reduced echelon formif the following conditions are satisfied: B) i and ii only. The dotted vertical line in each matrix should be a single vertical line.) i. Web the final matrix is in reduced row echelon form. Web how to solve a system in reduced echelon form. [ 1 0 0 1 0 1.
Solved Are the following matrices in Row Reduced Echelon
Row operation, row equivalence, matrix,. (a) the first nonzero element in each row (if any) is a 1 (a leading entry). The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated. Adding a constant times a row to another row: Any matrix can be transformed to reduced row echelon.
päta praktický Ovocná zelenina reduced row echelon form calculator
Adding a constant times a row to another row: If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: Row reduction we perform row operations to row reduce a..
Reduced Row Echelon Form Matrix Calculator CALCKP
Consider a linear system where is a matrix of coefficients, is an vector of unknowns, and is a vector of constants. If m is a sufficiently non ‐ degenerate. Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: [5] it is in row echelon form. Any matrix can be.
Solved Which of the following matrices are in rowreduced
Web the final matrix is in reduced row echelon form. Consider the matrix a given by. Web a 3×5 matrix in reduced row echelon form. Using the three elementary row operations we may rewrite a in an echelon form as or, continuing with additional row operations, in the. [ 1 0 0 1 0 1.
Solved Question3 Which of the following matrices are in
Web a 3×5 matrix in reduced row echelon form. Row operation, row equivalence, matrix,. Web a matrix is in row reduced echelon formif the following conditions are satisfied: Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: Consider a linear system where is a matrix of coefficients, is an.
Solved Classify The Following Matrices As To Whether They...
Web give one reason why one might not be interested in putting a matrix into reduced row echelon form. The dotted vertical line in each matrix should be a single vertical line.) i. Consider a linear system where is a matrix of coefficients, is an vector of unknowns, and is a vector of constants. Web then there exists an invertible.
Augmented Matrices Reduced Row Echelon Form YouTube
If m is a sufficiently non ‐ degenerate. Adding a constant times a row to another row: Web a 3×5 matrix in reduced row echelon form. If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. Using the three elementary row operations we may rewrite a in an echelon.
Transforming Square Matrices Into Reduced Row Echelon Form 7 Steps
If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. Using the three elementary row operations we may rewrite a in an echelon form as or, continuing with additional row operations, in the. [5] it is in row echelon form. The dotted vertical line in each matrix should be.
Solved Question 3 Which of the following matrices are in row
If m is a sufficiently non ‐ degenerate. Web give one reason why one might not be interested in putting a matrix into reduced row echelon form. Identify the leading 1s in the following matrix: Web then there exists an invertible matrix p such that pa = r and an invertible matrix q such that qr^t qrt is the reduced.
Solved (1) Use Gaussian Elimination To Put The Following
Transformation of a matrix to reduced row echelon form. Using the three elementary row operations we may rewrite a in an echelon form as or, continuing with additional row operations, in the. Web the final matrix is in reduced row echelon form. Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the.
Web How To Solve A System In Reduced Echelon Form.
The leading entry in each nonzero. If m is a non ‐ degenerate square matrix, rowreduce [ m ] is identitymatrix [ length [ m ] ]. Row operation, row equivalence, matrix,. This problem has been solved!.
Web A Matrix Is In Row Reduced Echelon Formif The Following Conditions Are Satisfied:
Web give one reason why one might not be interested in putting a matrix into reduced row echelon form. Row reduction we perform row operations to row reduce a. Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. Web then there exists an invertible matrix p such that pa = r and an invertible matrix q such that qr^t qrt is the reduced row echelon form of r^t rt.
Using The Three Elementary Row Operations We May Rewrite A In An Echelon Form As Or, Continuing With Additional Row Operations, In The.
Transformation of a matrix to reduced row echelon form. Any matrix can be transformed to reduced row echelon form, using a. [5] it is in row echelon form. The row reduced form given the matrix \(a\) we apply elementary row operations until each nonzero below the diagonal is eliminated.
[ 1 0 0 1 0 1.
Web a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: Web the final matrix is in reduced row echelon form. Identify the leading 1s in the following matrix: Consider the matrix a given by.