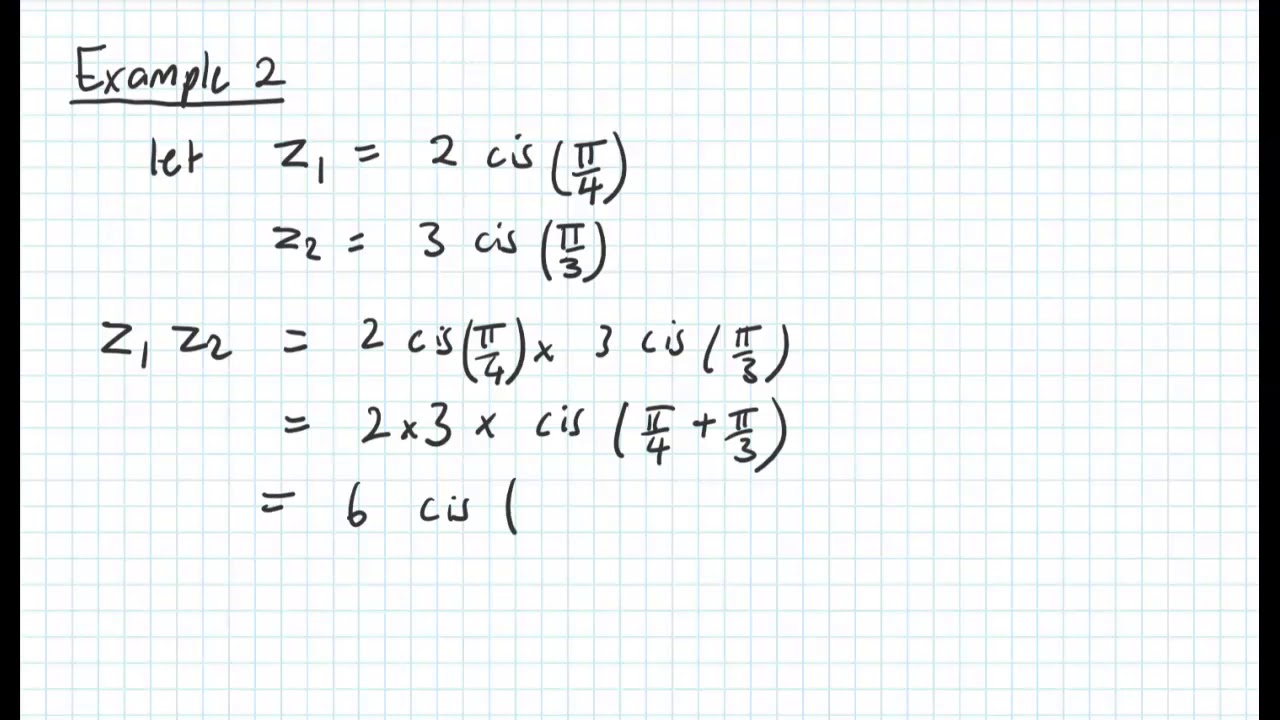How To Multiply Complex Numbers In Polar Form
How To Multiply Complex Numbers In Polar Form - Web 2 answers sorted by: See example \(\pageindex{4}\) and example \(\pageindex{5}\). (a+bi) (c+di) = (ac−bd) + (ad+bc)i example: [ r 1 ( cos θ 1 + i sin θ 1)] [ r 2 ( cos θ 2 + i sin θ 2)] = r 1 r 2 ( cos θ 1 cos θ 2 −. Web to multiply/divide complex numbers in polar form, multiply/divide the two moduli and add/subtract the arguments. Multiply & divide complex numbers in polar form. Multiplication by j10 or by j30 will cause the vector to rotate anticlockwise by the. Web visualizing complex number multiplication. It is just the foil method after a little work: Web learn how to convert a complex number from rectangular form to polar form.
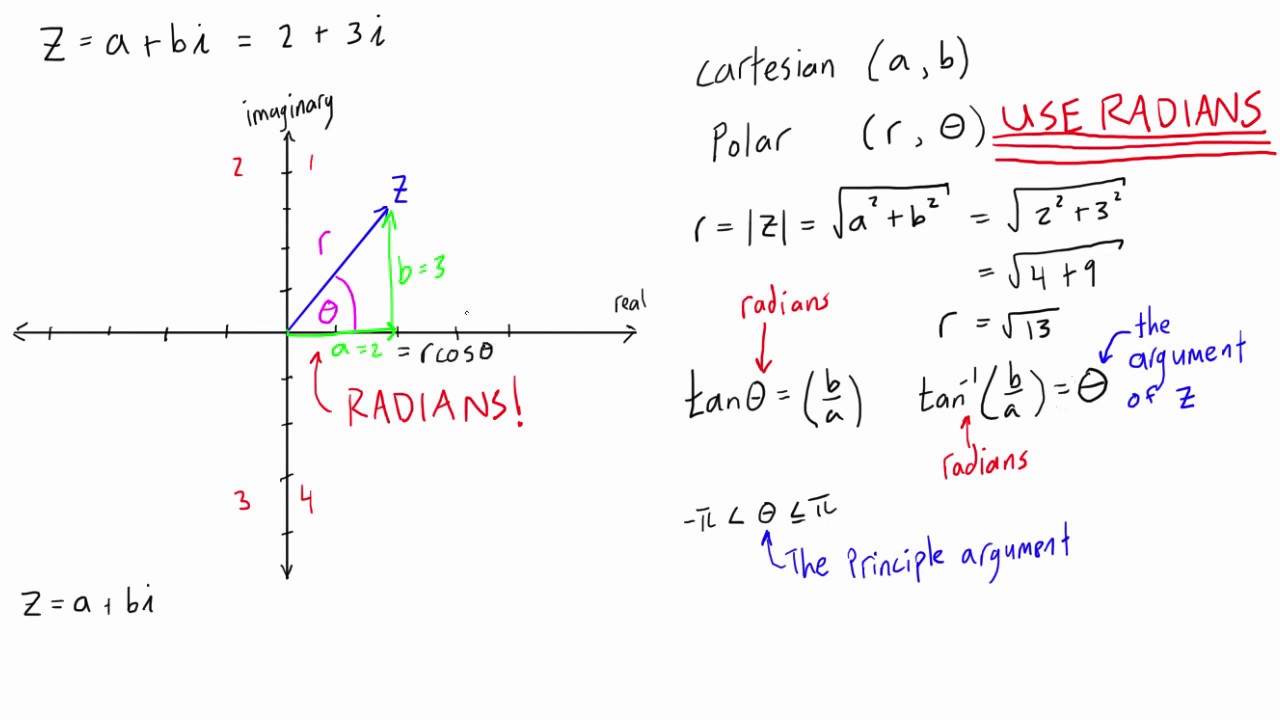
Given two complex numbers in the polar form z 1 = r 1 ( cos ( θ 1) + i sin ( θ 1)) and z 2 = r 2 ( cos ( θ 2) +. More specifically, for any two complex numbers, z 1 = r 1 ( c o s ( θ 1) + i s i n ( θ 1)) and z 2 = r 2 ( c o s ( θ 2) + i s i n ( θ 2)), we have: Web so by multiplying an imaginary number by j2 will rotate the vector by 180o anticlockwise, multiplying by j3 rotates it 270o and by j4 rotates it 360o or back to its original position. 13 by multiplying things out as usual, you get [r1(cosθ1 + i sinθ1)][r2(cosθ2 + i sinθ2)] = r1r2(cosθ1 cosθ2 − sinθ1 sinθ2 + i[sinθ1 cosθ2 + sinθ2 cosθ1]). [ r 1 ( cos θ 1 + i sin θ 1)] [ r 2 ( cos θ 2 + i sin θ 2)] = r 1 r 2 ( cos θ 1 cos θ 2 −. Web 2 answers sorted by: And there you have the (ac − bd) + (ad + bc)i pattern. Web visualizing complex number multiplication. This rule is certainly faster,. Web to write complex numbers in polar form, we use the formulas \(x=r \cos \theta\), \(y=r \sin \theta\), and \(r=\sqrt{x^2+y^2}\).
Z1 ⋅ z2 = |z1 ⋅|z2| z 1 · z 2 = | z 1 · | z 2 |. Given two complex numbers in the polar form z 1 = r 1 ( cos ( θ 1) + i sin ( θ 1)) and z 2 = r 2 ( cos ( θ 2) +. Web the figure below shows the geometric multiplication of the complex numbers 2 +2i 2 + 2 i and 3+1i 3 + 1 i. Web to write complex numbers in polar form, we use the formulas \(x=r \cos \theta\), \(y=r \sin \theta\), and \(r=\sqrt{x^2+y^2}\). [ r 1 ( cos θ 1 + i sin θ 1)] [ r 2 ( cos θ 2 + i sin θ 2)] = r 1 r 2 ( cos θ 1 cos θ 2 −. Sum the values of θ 1 and θ 2. For multiplication in polar form the following applies. To divide, divide the magnitudes and. To multiply complex numbers in polar form, multiply the magnitudes and add the angles. Web to add complex numbers in rectangular form, add the real components and add the imaginary components.
Complex Numbers Multiplying in Polar Form YouTube
And there you have the (ac − bd) + (ad + bc)i pattern. For multiplication in polar form the following applies. More specifically, for any two complex numbers, z 1 = r 1 ( c o s ( θ 1) + i s i n ( θ 1)) and z 2 = r 2 ( c o s ( θ.
Multiply Polar Form Complex Numbers YouTube
To multiply complex numbers in polar form, multiply the magnitudes and add the angles. To divide, divide the magnitudes and. W1 = a*(cos(x) + i*sin(x)). Substitute the products from step 1 and step 2 into the equation z p = z 1 z 2 = r 1 r 2 ( cos ( θ 1 + θ 2). Web in this.
Polar form Multiplication and division of complex numbers YouTube
Multiplication of these two complex numbers can be found using the formula given below:. Hernandez shows the proof of how to multiply complex number in polar form, and works. 1 2 3 4 1 2 3 4 5 6 7 8 9. Sum the values of θ 1 and θ 2. Z1z2=r1r2 (cos (θ1+θ2)+isin (θ1+θ2)) let's do.
How to Multiply Complex Numbers in Polar Form? YouTube
But i also would like to know if it is really correct. This rule is certainly faster,. Sum the values of θ 1 and θ 2. Web to multiply/divide complex numbers in polar form, multiply/divide the two moduli and add/subtract the arguments. Web the figure below shows the geometric multiplication of the complex numbers 2 +2i 2 + 2 i.
How to write a complex number in polar form YouTube
Multiply & divide complex numbers in polar form. Web multiplication of complex numbers in polar form. The result is quite elegant and simpler than you think! Substitute the products from step 1 and step 2 into the equation z p = z 1 z 2 = r 1 r 2 ( cos ( θ 1 + θ 2). This rule.
Complex Numbers Multiplying and Dividing in Polar Form, Ex 1 YouTube
W1 = a*(cos(x) + i*sin(x)). Web to add complex numbers in rectangular form, add the real components and add the imaginary components. But i also would like to know if it is really correct. To multiply complex numbers in polar form, multiply the magnitudes and add the angles. Web so by multiplying an imaginary number by j2 will rotate the.
How to find the product Vtext multiply divide complex numbers polar
[ r 1 ( cos θ 1 + i sin θ 1)] [ r 2 ( cos θ 2 + i sin θ 2)] = r 1 r 2 ( cos θ 1 cos θ 2 −. Z1 ⋅ z2 = |z1 ⋅|z2| z 1 · z 2 = | z 1 · | z 2 |. Web so by.
Multiplying Complex Numbers in Polar Form YouTube
It is just the foil method after a little work: More specifically, for any two complex numbers, z 1 = r 1 ( c o s ( θ 1) + i s i n ( θ 1)) and z 2 = r 2 ( c o s ( θ 2) + i s i n ( θ 2)), we have:.
Multiplying Complex Numbers in Polar Form YouTube
To divide, divide the magnitudes and. Web to write complex numbers in polar form, we use the formulas \(x=r \cos \theta\), \(y=r \sin \theta\), and \(r=\sqrt{x^2+y^2}\). Web visualizing complex number multiplication. Complex number polar form review. (a+bi) (c+di) = (ac−bd) + (ad+bc)i example:
Multiplying complex numbers (polar form) YouTube
Web to write complex numbers in polar form, we use the formulas \(x=r \cos \theta\), \(y=r \sin \theta\), and \(r=\sqrt{x^2+y^2}\). Sum the values of θ 1 and θ 2. Hernandez shows the proof of how to multiply complex number in polar form, and works. See example \(\pageindex{4}\) and example \(\pageindex{5}\). To multiply complex numbers in polar form, multiply the magnitudes.
Web To Multiply/Divide Complex Numbers In Polar Form, Multiply/Divide The Two Moduli And Add/Subtract The Arguments.
Suppose z 1 = r 1 (cos θ 1 + i sin θ 1) and z 2 = r 2 (cos θ 2 + i sin θ 2) are two complex numbers in polar form, then the product, i.e. To multiply complex numbers in polar form, multiply the magnitudes and add the angles. 13 by multiplying things out as usual, you get [r1(cosθ1 + i sinθ1)][r2(cosθ2 + i sinθ2)] = r1r2(cosθ1 cosθ2 − sinθ1 sinθ2 + i[sinθ1 cosθ2 + sinθ2 cosθ1]). Z1 ⋅ z2 = |z1 ⋅|z2| z 1 · z 2 = | z 1 · | z 2 |.
Web Visualizing Complex Number Multiplication.
Web i'll show here the algebraic demonstration of the multiplication and division in polar form, using the trigonometric identities, because not everyone looks at the tips and thanks tab. Then, \(z=r(\cos \theta+i \sin \theta)\). Web to add complex numbers in rectangular form, add the real components and add the imaginary components. Web 2 answers sorted by:
Multiply & Divide Complex Numbers In Polar Form.
W1 = a*(cos(x) + i*sin(x)). Given two complex numbers in the polar form z 1 = r 1 ( cos ( θ 1) + i sin ( θ 1)) and z 2 = r 2 ( cos ( θ 2) +. Z1z2=r1r2 (cos (θ1+θ2)+isin (θ1+θ2)) let's do. Complex number polar form review.
Sum The Values Of Θ 1 And Θ 2.
Substitute the products from step 1 and step 2 into the equation z p = z 1 z 2 = r 1 r 2 ( cos ( θ 1 + θ 2). Web in this video, i demonstrate how to multiply 2 complex numbers expressed in their polar forms. More specifically, for any two complex numbers, z 1 = r 1 ( c o s ( θ 1) + i s i n ( θ 1)) and z 2 = r 2 ( c o s ( θ 2) + i s i n ( θ 2)), we have: Web multiplication of complex numbers in polar form.